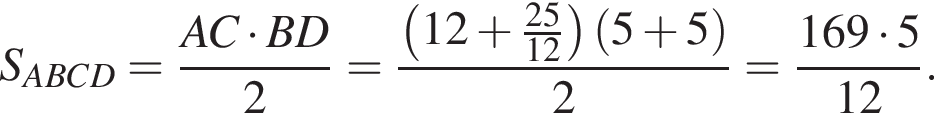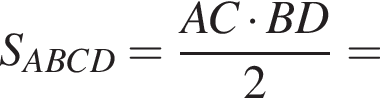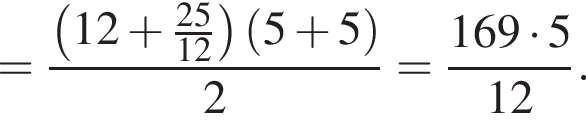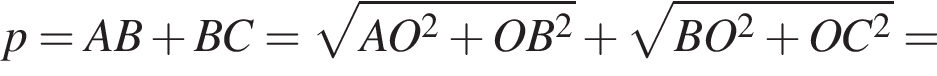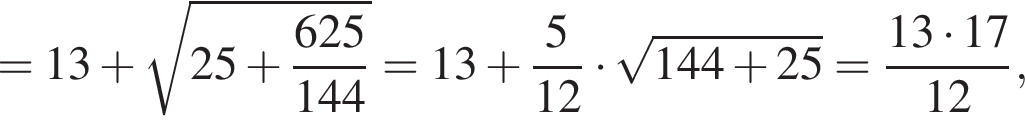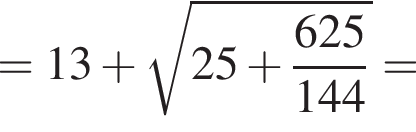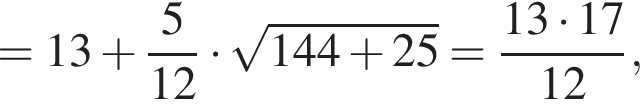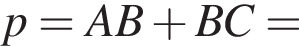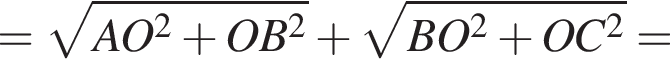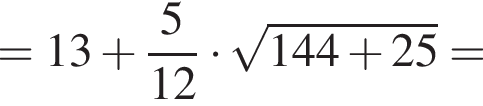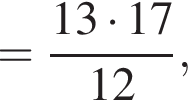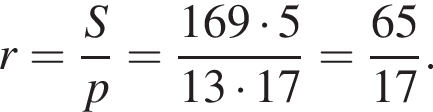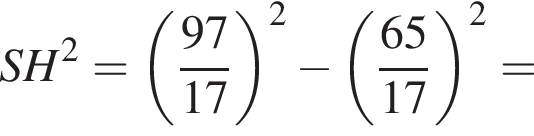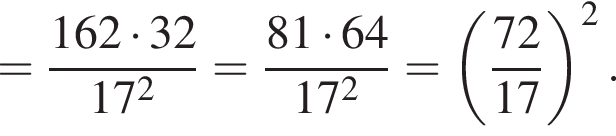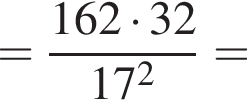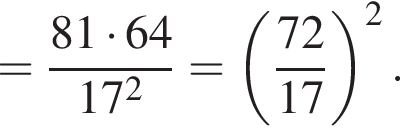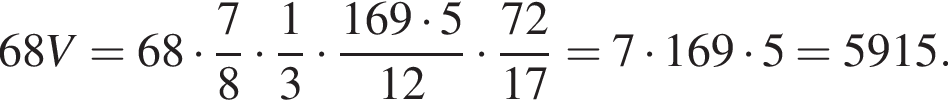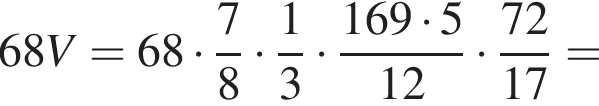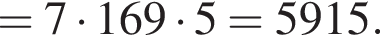Треугольник ABC — равнобедренный с основанием BC. Используя данные рисунка, найдите градусную меру угла BCA треугольника ABC.
Централизованное тестирование по математике, 2021
Среди дробей ![]()
![]()
![]()
![]()
![]() укажите ту, которая равна дроби
укажите ту, которая равна дроби ![]()
Даны пары значений переменных x и y: (5; 3); (10; −2); (−9; 1); (2; 6); (8; 0). Укажите пару, которая НЕ является решением уравнения x + y = 8.
Среди чисел 0; −6; −3; −11; 11 укажите то, которое не меньше −9 и не больше −4.
Точка С делит отрезок АВ в отношении 7 : 2, считая от точки B. Если длина отрезка АВ равна 27, то длина отрезка AC равна:
В магазин поступило 29 коробок с маслом по 80 пачек масла в каждой. Какое наибольшее количество пачек масла необходимо продавать ежедневно, чтобы масло было распродано не менее чем за 60 дней?
На рисунке изображен график функции y = f(x), которая определена на промежутке [−5; 5]. Найдите количество целых значений x, при которых выполняется неравенство 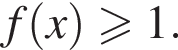 (Черными точками отмечены узлы сетки, через которые проходит график, функции y = f(x).
(Черными точками отмечены узлы сетки, через которые проходит график, функции y = f(x).
Результат упрощения выражения 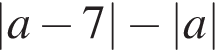 при
при 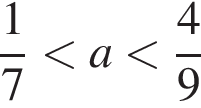 имеет вид:
имеет вид:
Значение выражения 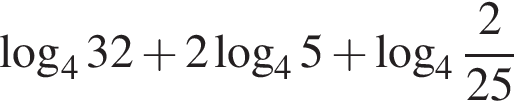 равно:
равно:

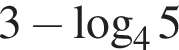
В первый день велосипедист проехал 45 км, а во второй день — на 12% больше, чем в первый. Сколько километров проехал велосипедист за два дня?
Найдите произведение координат точки пересечения прямых 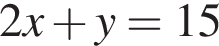 и
и 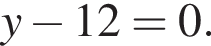
Укажите номера функций, которые являются четными.
| 1) y = 3 − 2x − x2; | 2) 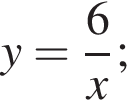 | 3) 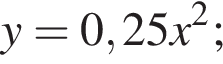 | 4)  | 5) 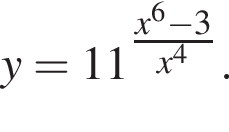 |
Площадь прямоугольного треугольника равна 7, а радиус описанной около него окружности равен R. Укажите номер формулы, которой может выражаться сумма катетов a и b.

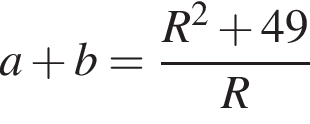
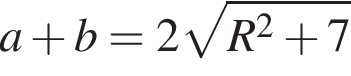
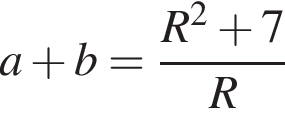
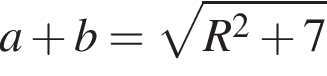
Основанием прямой треугольной призмы ABCA1B1C1 является треугольник АВС, в котором 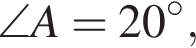
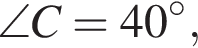 радиус описанной около него окружности равен
радиус описанной около него окружности равен ![]() Найдите длину диагонали грани AA1C1C, если площадь этой грани равна
Найдите длину диагонали грани AA1C1C, если площадь этой грани равна ![]()
Используя схематичное изображение параболы
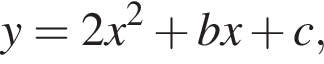 найдите сумму b + c.
найдите сумму b + c.
Укажите номера уравнений, которые являются равносильными:
1. 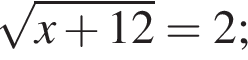
2. 
3. 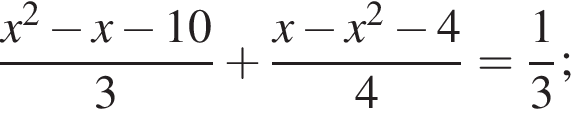
4. 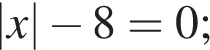
5. 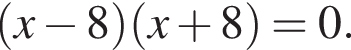
Точки А и В расположены в узлах сетки (см. рис.) и являются соседними вершинами квадрата АВСD. Найдите площадь квадрата ABСD.
SABCD — правильная четырехугольная пирамида, все ребра которой равны 54. Точка M — середина ребра SC. Точка  DN : NS = 1 : 3 (см. рис.). Найдите длину отрезка, по которому плоскость, проходящая через точки M и N параллельно ребру SB, пересекает основание ABCD пирамиды.
DN : NS = 1 : 3 (см. рис.). Найдите длину отрезка, по которому плоскость, проходящая через точки M и N параллельно ребру SB, пересекает основание ABCD пирамиды.
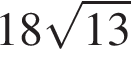
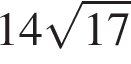
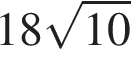
На диаграмме показано количество посещений сайта на протяжении недели (со вторника по воскресенье). Установите соответствие между вопросами А−В и ответами 1−6.
| Вопрос | Ответ |
|---|---|
A) В какой день недели было на 60 посещений больше, чем в предыдущий? Б) В какой день недели количество посещений было на 20% меньше, чем в среду? B) В какой день недели количество посещений было на 10% больше, чем в предыдущий? | 1) Вторник. 2) Среда. 3) Четверг. 4) Пятница. 5) Суббота. 6) Воскресенье. |
Ответ запишите в виде сочетания букв и цифр, соблюдая алфавитную последовательность букв левого столбца. Помните, что некоторые данные правого столбца могут использоваться несколько раз или не использоваться вообще. Например: А1Б1В4.
Выберите три верных утверждения:
1) если 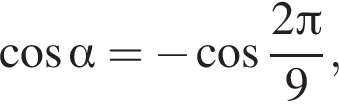 то
то 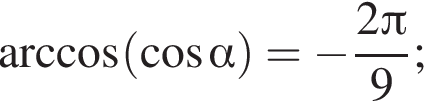
2) если 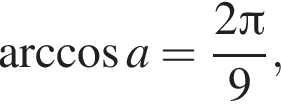 то
то 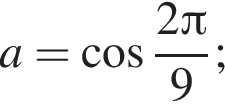
3) если 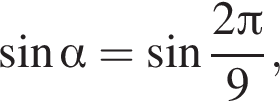 то
то 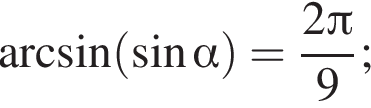
4) если 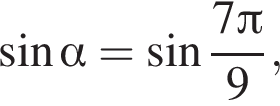 то
то 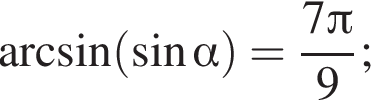
5) если 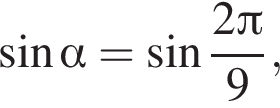 то
то 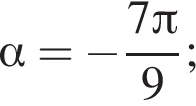
6) если 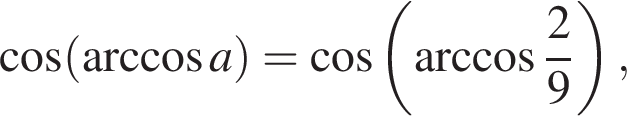 то
то 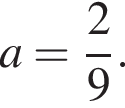
Ответ запишите цифрами (порядок записи цифр не имеет значения). Например: 123.
Выберите три верных утверждения, если известно, что две перпендикулярные плоскости
![]() и
и ![]() пересекаются по прямой a и точка A принадлежит плоскости
пересекаются по прямой a и точка A принадлежит плоскости ![]() (см. рис.).
(см. рис.).
1. Любая точка прямой a лежит в плоскостях ![]() и
и ![]()
2. Любая прямая, перпендикулярная прямой a, принадлежит плоскости ![]()
3. Существует единственная прямая, проходящая через точку A и перпендикулярная плоскости ![]()
4. Прямая, проходящая через точку A и перпендикулярная плоскости ![]() перпендикулярна плоскости
перпендикулярна плоскости ![]()
5. Существует прямая, проходящая через точку А перпендикулярно прямой а, перпендикулярная плоскости ![]()
6. Любая прямая, проходящая через точку A и пересекающая плоскость ![]() пересекает прямую a.
пересекает прямую a.
Ответ запишите цифрами (порядок записи цифр не имеет значения). Например: 123.
На пастбище квадратной формы загон для скота огорожен так, как показано на рисунке. Все размеры указаны в метрах. Найдите площадь загона (в м2), если площадь пастбища в 72 раза больше площади загона.
Найдите значение выражения 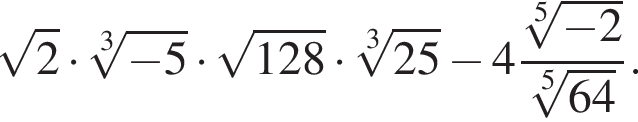
Площадь боковой поверхности цилиндра равна ![]() Найдите объем V цилиндра, если известно, что радиус его основания больше высоты на 6,5. В ответ запишите значение выражения
Найдите объем V цилиндра, если известно, что радиус его основания больше высоты на 6,5. В ответ запишите значение выражения ![]()
Решите уравнение 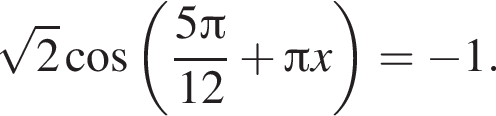 В ответ запишите увеличенное в 2 раза произведение наибольшего корня (в радианах) на количество корней этого уравнения на промежутке [7; 13].
В ответ запишите увеличенное в 2 раза произведение наибольшего корня (в радианах) на количество корней этого уравнения на промежутке [7; 13].
Найдите сумму всех целых решений неравенства 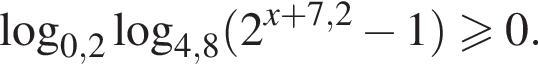
АС — общая гипотенуза прямоугольных треугольников ABC и ADC. Плоскости этих треугольников взаимно перпендикулярны. Найдите квадрат длины отрезка BD, если 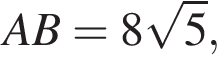
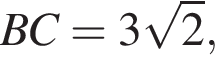 AD = DC.
AD = DC.
Числовая последовательность (an) задана формулой n-го члена 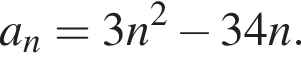 Найдите наименьший член am этой последовательности и его номер m. В ответ запишите значение выражения m · am.
Найдите наименьший член am этой последовательности и его номер m. В ответ запишите значение выражения m · am.
Найдите увеличенную в 25 раз сумму квадратов корней уравнения
Прямая, проходящая через вершину N треугольника KMN, делит его медиану KA в отношении 3 : 7, считая от вершины K, и пересекает сторону KM в точке B. Найдите площадь треугольника KMN, если площадь треугольника NKB равна 15.
Петя записал на доске два различных натуральных числа. Затем он их сложил, перемножил, вычел из большего записанного числа меньшее и разделил большее на меньшее. Сложив четыре полученных результата, Петя получил число 1089. Найдите все такие пары натуральных чисел. В ответ запишите их сумму.
Основанием пирамиды SABCD является выпуклый четырехугольник ABCD, диагонали АС и BD которого перпендикулярны и пересекаются в точке O, АО = 12, 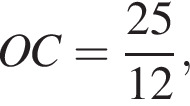 ВО = OD = 5. Вершина S пирамиды SABCD удалена на расстояние
ВО = OD = 5. Вершина S пирамиды SABCD удалена на расстояние ![]() от каждой из прямых AB, BC, СD и AD. Через середину высоты пирамиды SABCD параллельно ее основанию проведена секущая плоскость, которая делит пирамиду на две части. Найдите значение выражения 68 · V, где V — объем большей из частей.
от каждой из прямых AB, BC, СD и AD. Через середину высоты пирамиды SABCD параллельно ее основанию проведена секущая плоскость, которая делит пирамиду на две части. Найдите значение выражения 68 · V, где V — объем большей из частей.

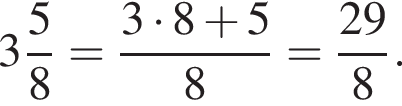
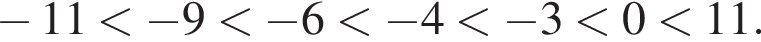
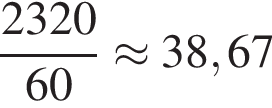 пачек масла. Поскольку необходимо найти, какое наибольшее количество пачек масла необходимо продавать ежедневно, чтобы масло было распродано не менее чем за 60 дней, ответ — 38.
пачек масла. Поскольку необходимо найти, какое наибольшее количество пачек масла необходимо продавать ежедневно, чтобы масло было распродано не менее чем за 60 дней, ответ — 38.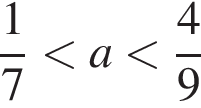 :
:
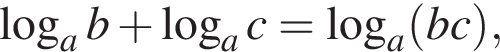 получаем:
получаем: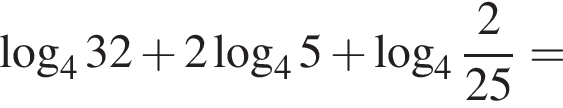
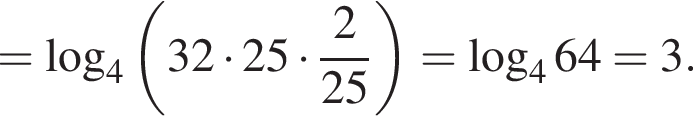
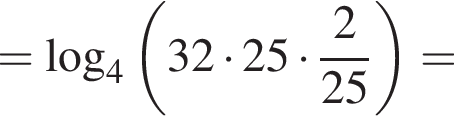
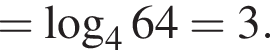
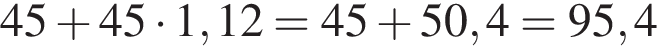 км.
км.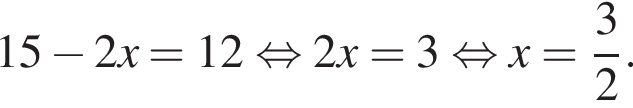
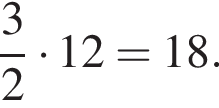
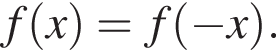 Проверим каждую функцию:
Проверим каждую функцию: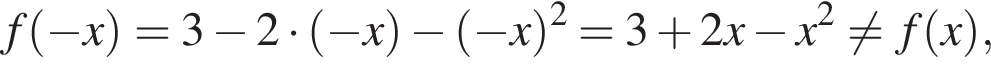
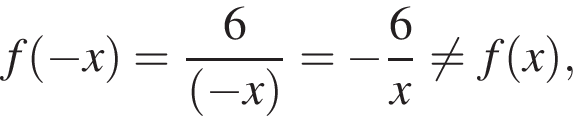
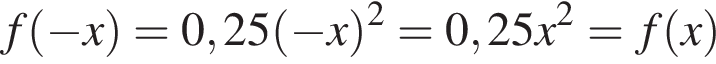 — чётная функция,
— чётная функция,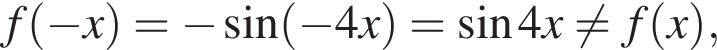
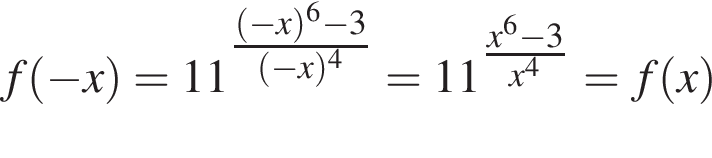 — чётная функция.
— чётная функция.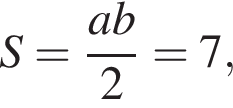 откуда ab = 14. Заметим, что по свойству окружности, описанной вокруг прямоугольного треугольника, длина гипотенузы равна 2R, тогда
откуда ab = 14. Заметим, что по свойству окружности, описанной вокруг прямоугольного треугольника, длина гипотенузы равна 2R, тогда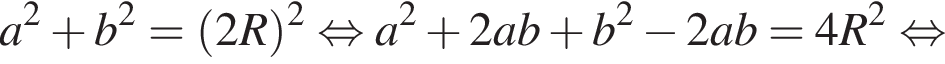

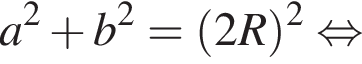
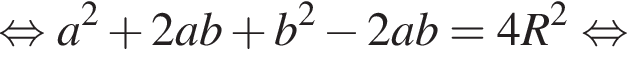
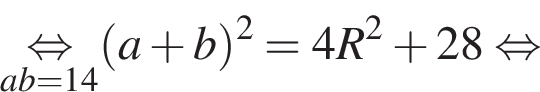
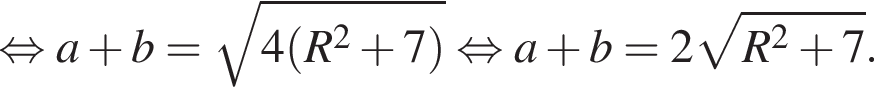
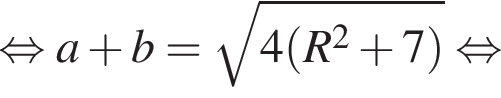
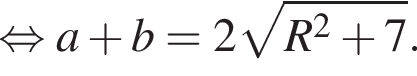
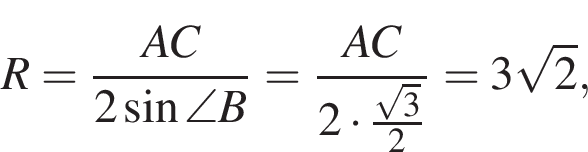
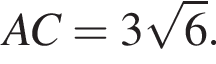 Тогда
Тогда 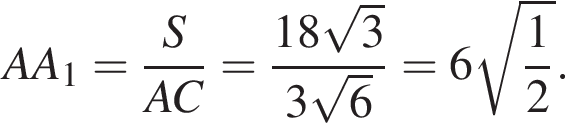 Окончательно, поскольку призма прямая, найдём длину искомой диагонали AC1 по теореме Пифагора:
Окончательно, поскольку призма прямая, найдём длину искомой диагонали AC1 по теореме Пифагора: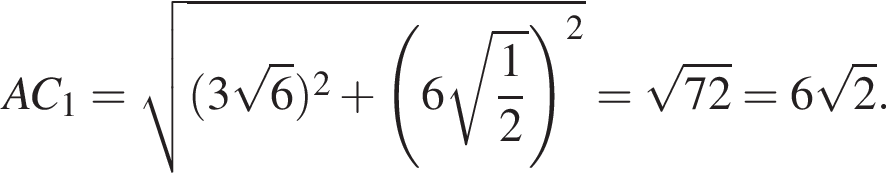
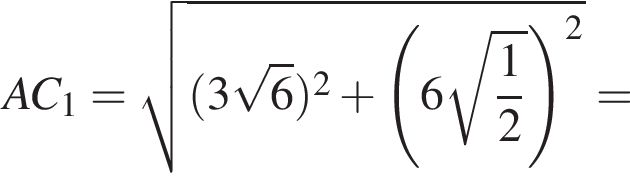
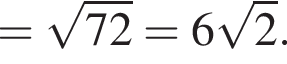
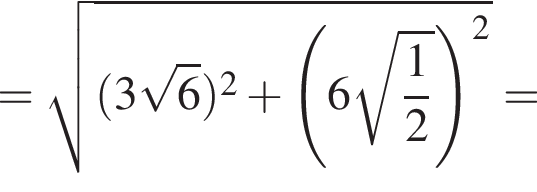
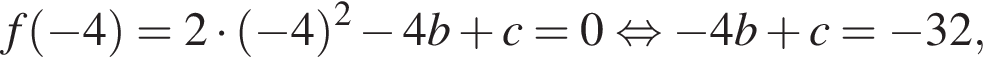
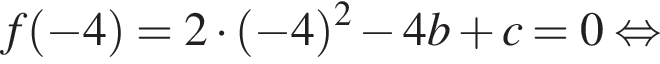
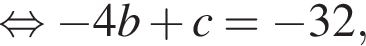
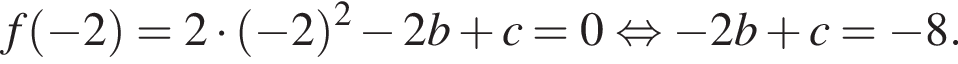
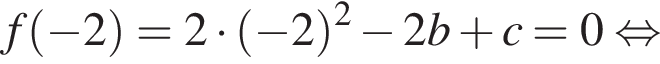

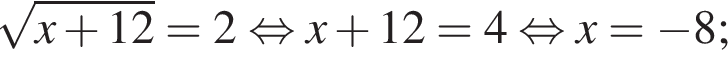
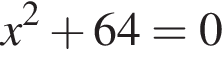 — корней нет;
— корней нет;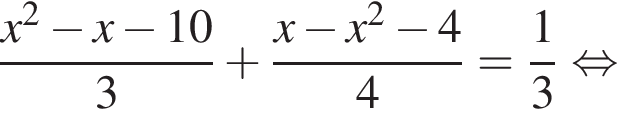
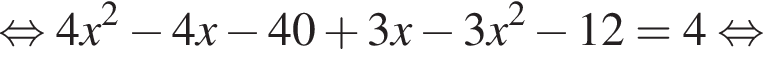
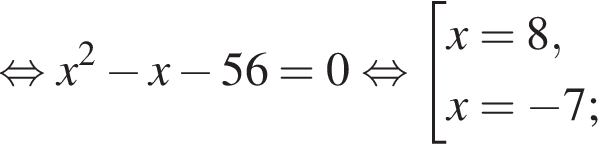
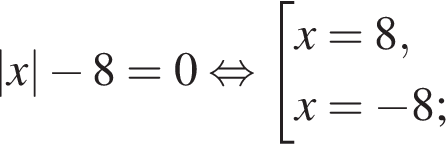
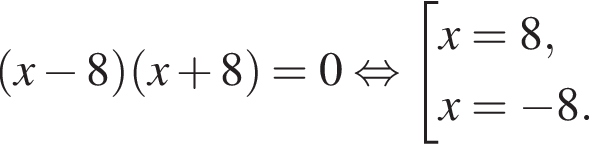
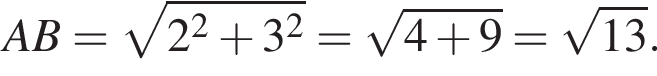

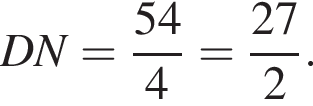 Заметим, что DN — средняя линия треугольника MFP, следовательно, D — середина отрезка FP, тогда, поскольку FD = DP = 27, CP = 27 · 3 = 81.
Заметим, что DN — средняя линия треугольника MFP, следовательно, D — середина отрезка FP, тогда, поскольку FD = DP = 27, CP = 27 · 3 = 81.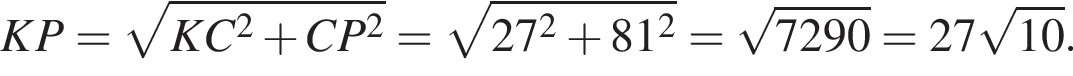
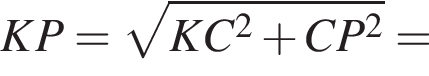

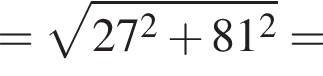
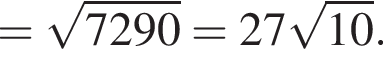
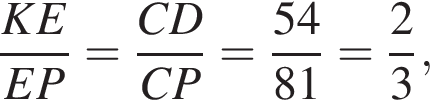
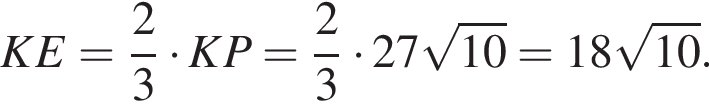
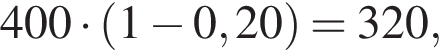 значит, количество посещений на 20% меньше, чем во вторник было в пятницу (4).
значит, количество посещений на 20% меньше, чем во вторник было в пятницу (4).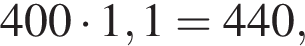 значит, в четверг количество посещений было на 10% больше, чем в предыдущий (3).
значит, в четверг количество посещений было на 10% больше, чем в предыдущий (3).
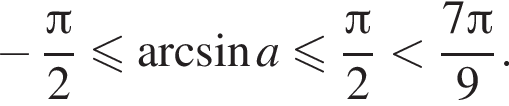
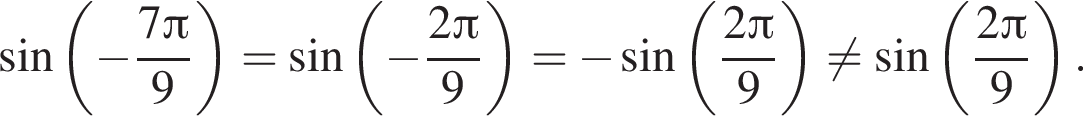
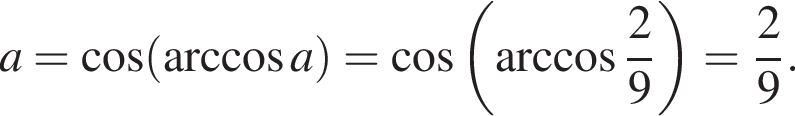
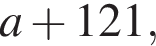 т. е.
т. е. 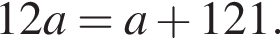 Откуда
Откуда 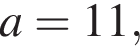 а площадь загона равна
а площадь загона равна 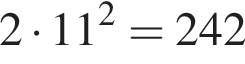 м2.
м2.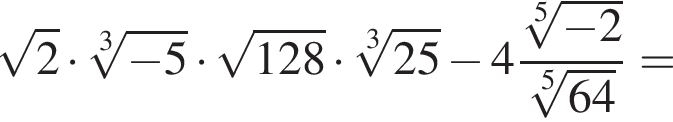
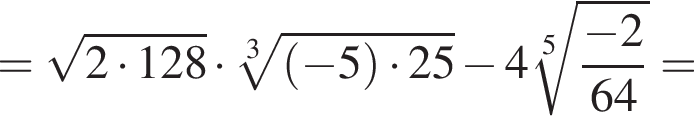
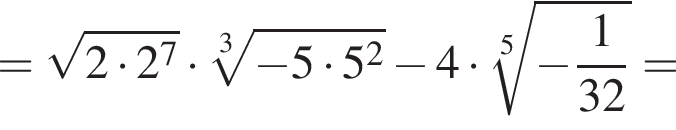
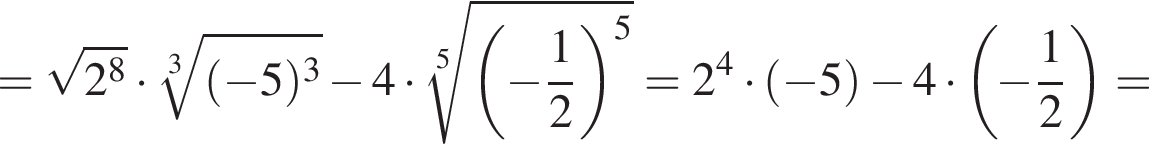
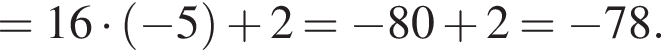
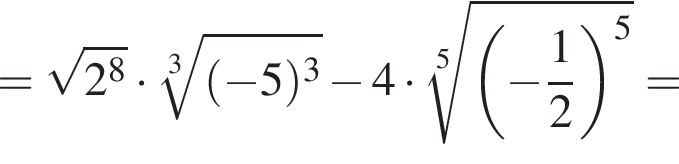
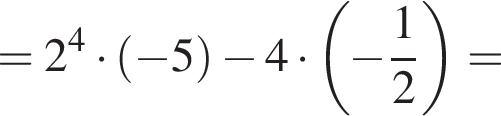
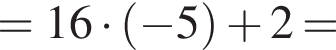
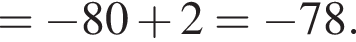
 по условию
по условию  а
а 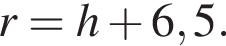 Тогда
Тогда
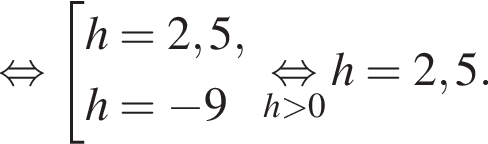

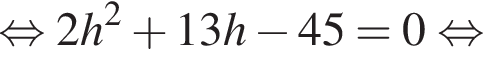
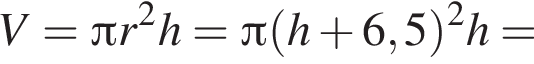
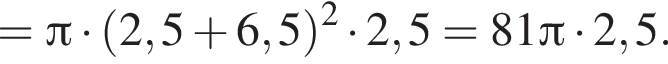
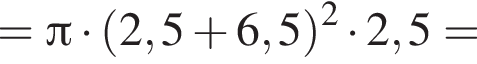

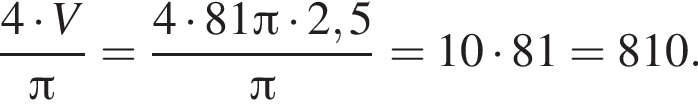
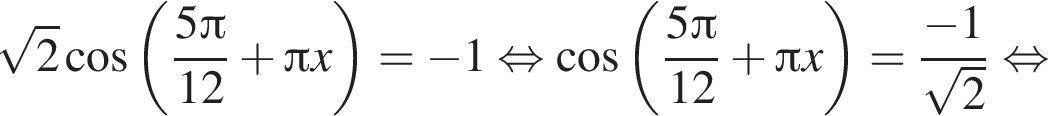

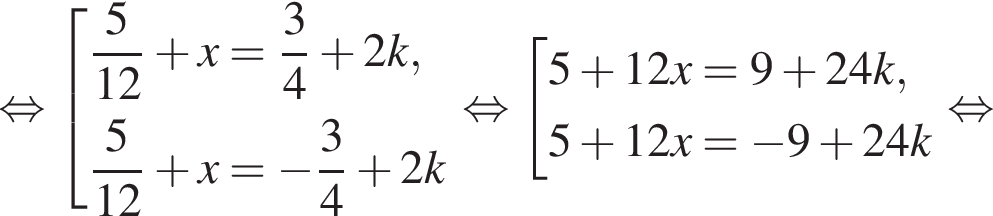
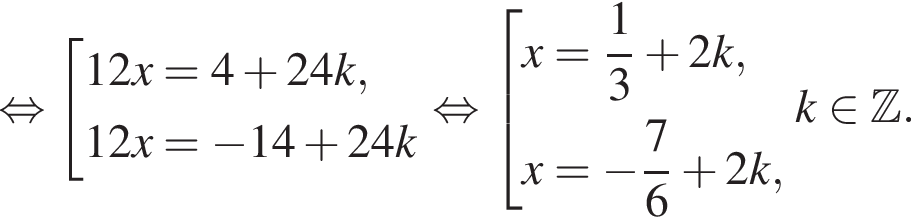
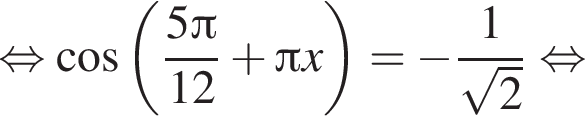
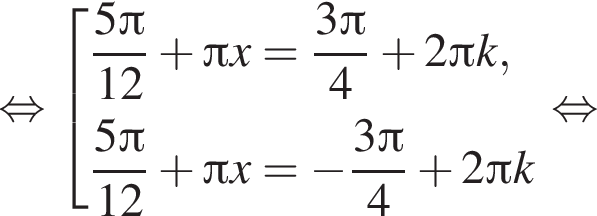
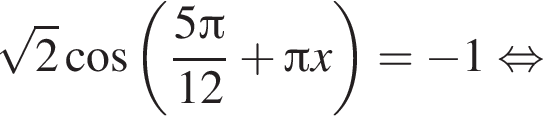
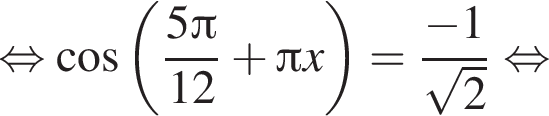
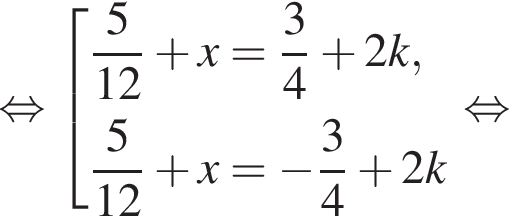
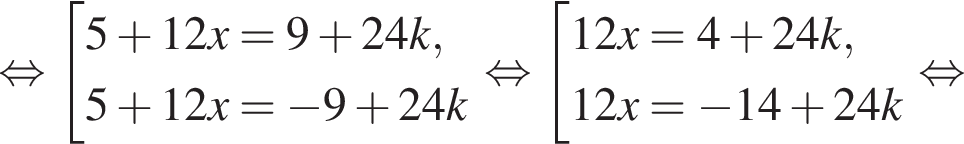
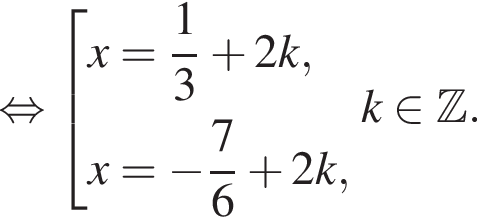
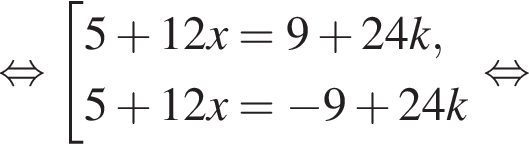
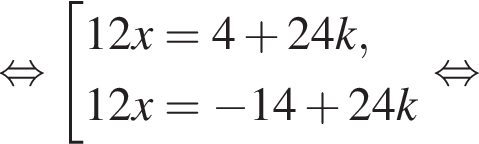
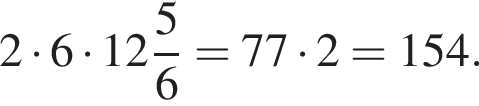
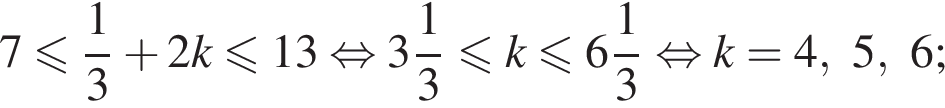
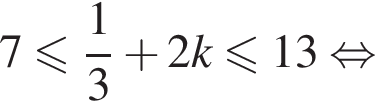
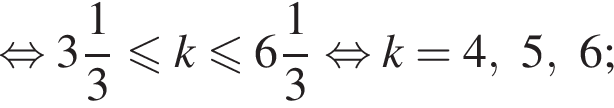
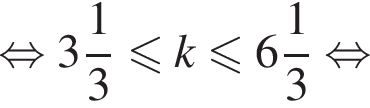
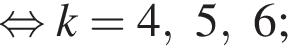
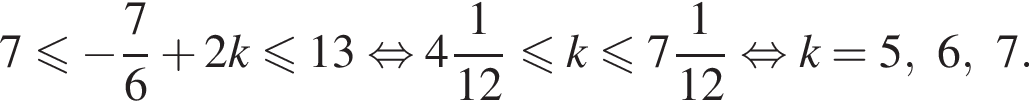
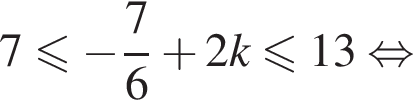
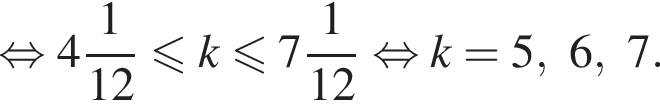
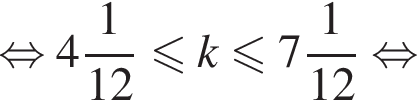
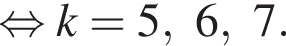
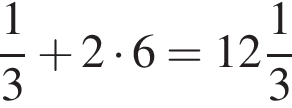 и
и 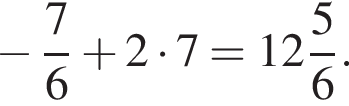 Тем самым больший корень на отрезке [7; 13] равен
Тем самым больший корень на отрезке [7; 13] равен 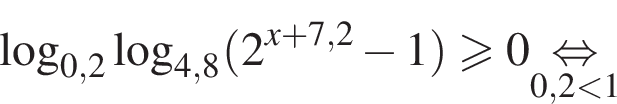
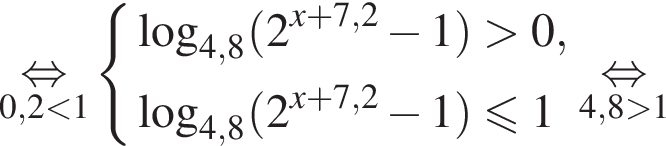
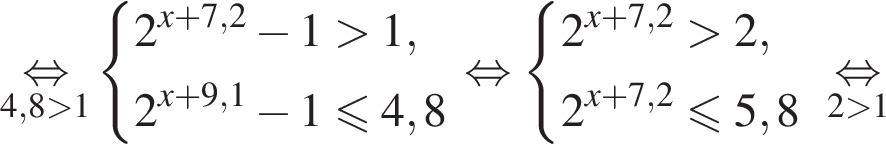
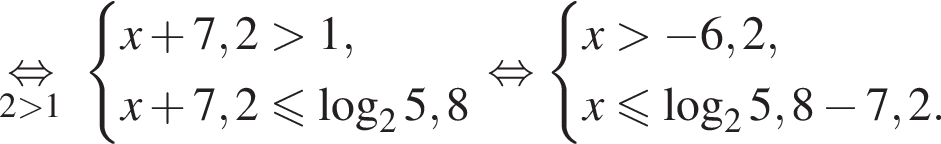
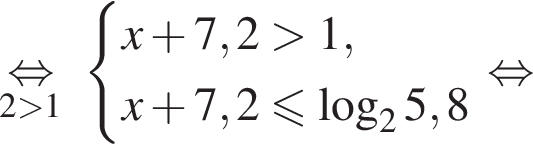
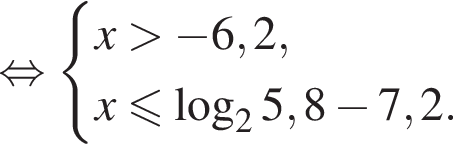
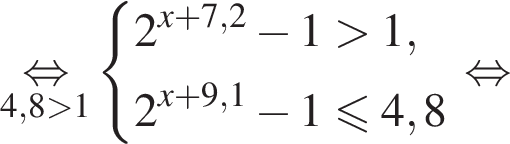
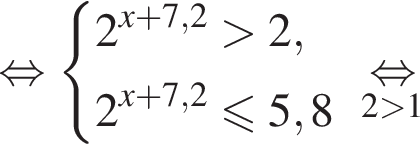
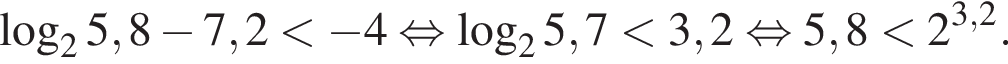
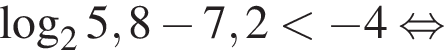
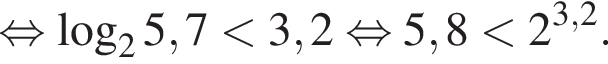
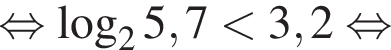
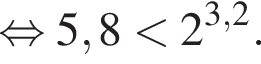
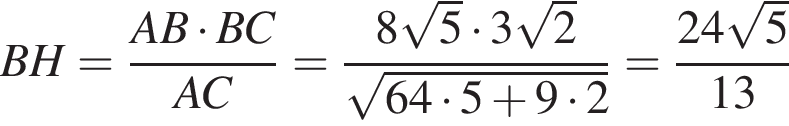
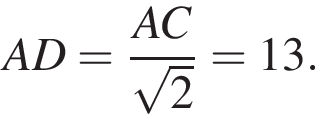 Значит,
Значит, 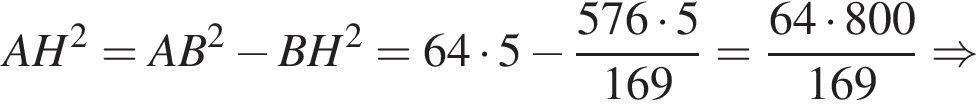
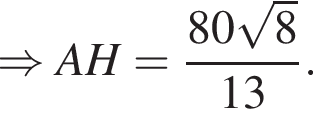
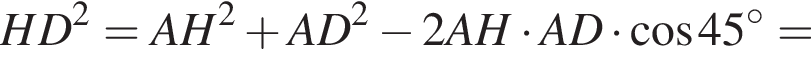
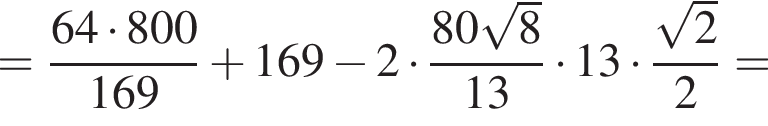
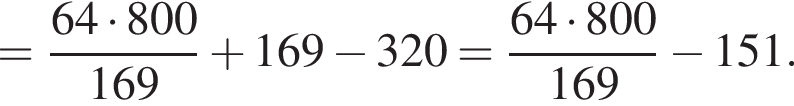


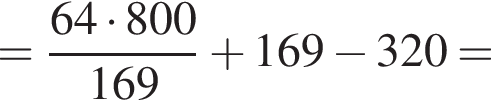
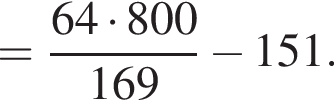
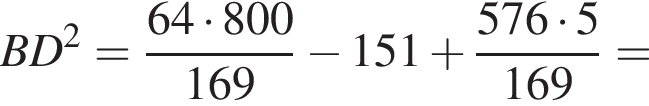
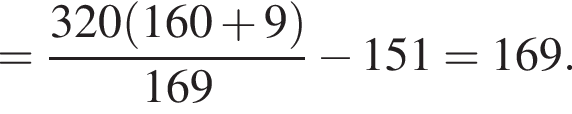
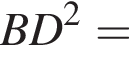
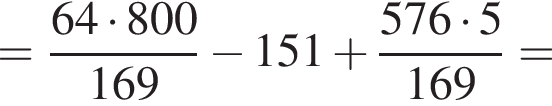
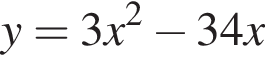 представляет собой параболу ветвями вверх. Поэтому наименьшее значение этой функции достигается при
представляет собой параболу ветвями вверх. Поэтому наименьшее значение этой функции достигается при  и значения тем больше, чем дальше x от этого числа. Значит, нужно найти ближайшее к
и значения тем больше, чем дальше x от этого числа. Значит, нужно найти ближайшее к 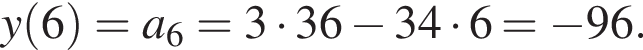 Тогда
Тогда 
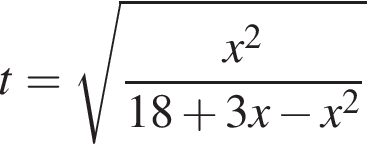 при
при 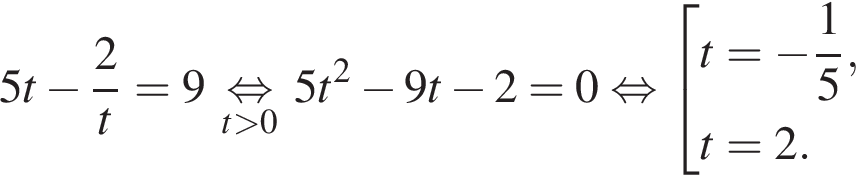
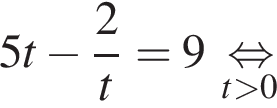
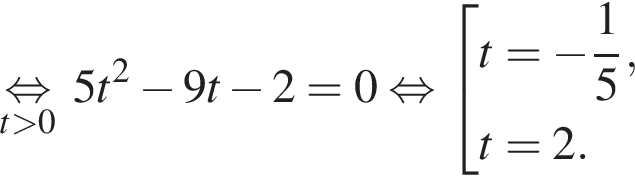
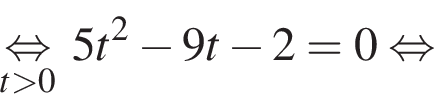
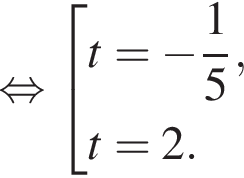
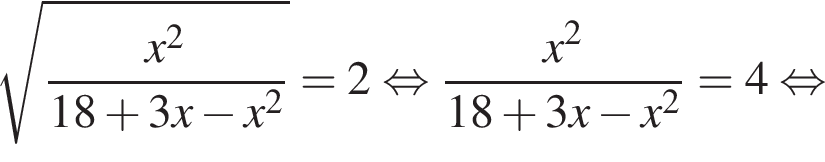
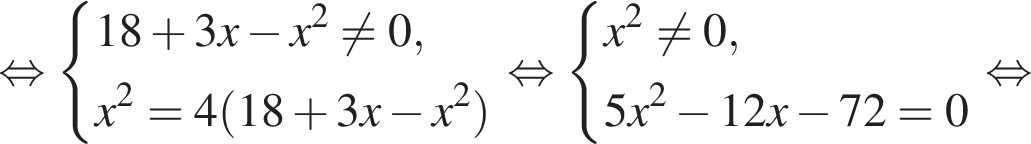
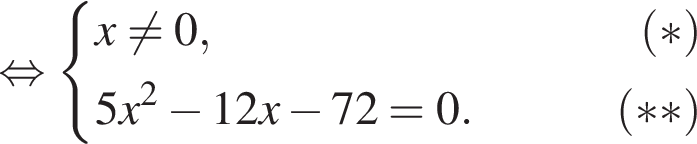
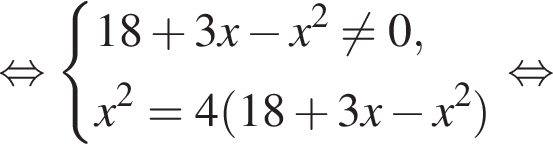
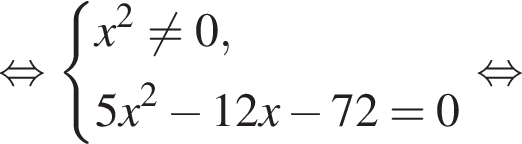
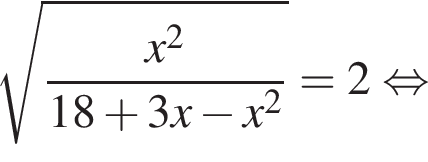
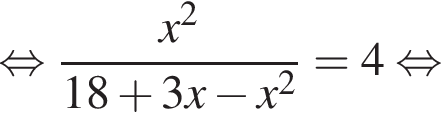
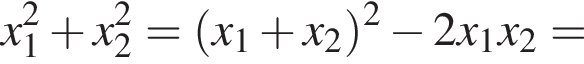
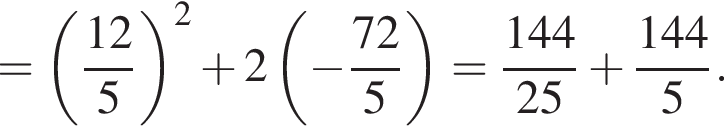
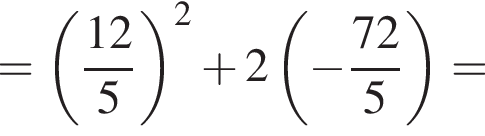
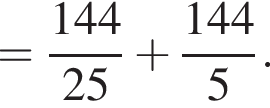
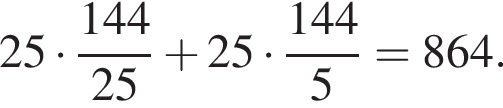
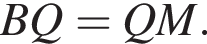 По теореме о пропорциональных отрезках получаем, что
По теореме о пропорциональных отрезках получаем, что 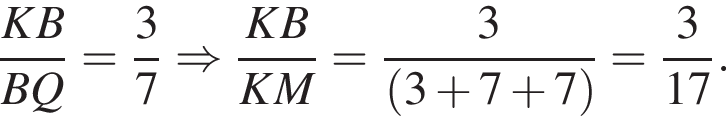
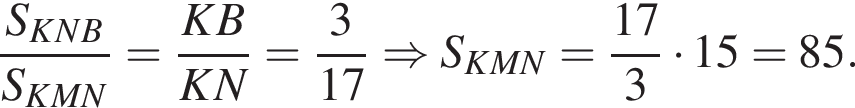

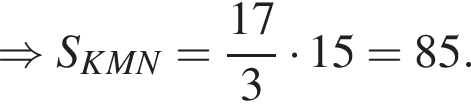
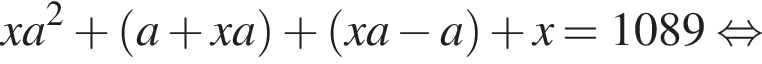
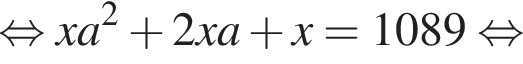
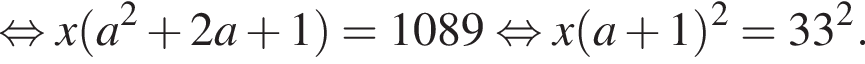
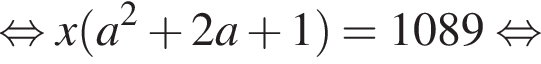
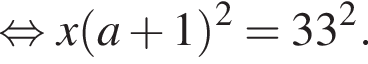
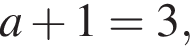
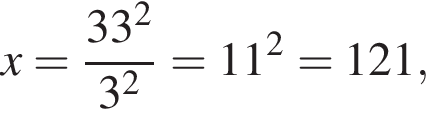
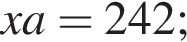
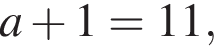
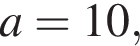
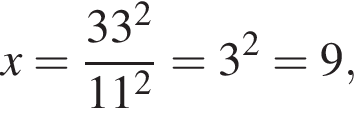
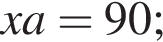
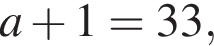
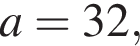
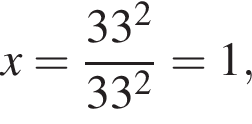
 что запрещено по условию.
что запрещено по условию.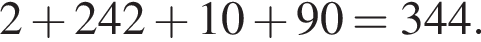
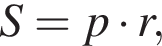 где p — полупериметр. Находим:
где p — полупериметр. Находим: